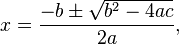Here's a few more I'm struggling with:
1) Two airplanes are leaving Chicago at the same time, one bound for New York and the other for California. The one heading to California has a tail wind and is thus going 25 MPH faster than the one headed for New York. If after one hour they are 575 miles apart, what are their speeds?
This one is just a matter of interpreting the words into their mathematical equivalent. Let's start with the fact that distance (d) is equal to velocity (v) multiplied by the time (t) spent at that velocity.
d = v*t
In this case, the total distance between the planes is equal to the distance traveled by plane 1 plus the distance traveled by plane 2 since we can assume they are travelling in opposite directions. And since we know their total distance apart, we add the two distances together and write:
d = v1*t + v2*t where v1 and v2 are the velocities of the two planes.
We can do a little bit of simplification and change that to:
d = t * (v1 + v2)
Almost there! Since the problem states that one plane is going 25mph faster than the other, we know that
v2 = v1 +25. Substituting that value in for v2, we get:
d = t * (v1 + v1 + 25) = t * (2 * v1 +25)
Now we know that the distance is 575 miles, and the time spent in the air was 1 hour so...
575 = 1 * (2 * v1 + 25) = 2* v1 + 25
Subtract 25 from both sides to get
550 = 2 * v1
Divide both sides by 2, and the final result is:
v1 = 225
Since we said before that
v2 = v1 + 25, we know that
v2 = 250.
So the answer is that the planes were flying 225mph and 250 mph.
2) How many ounces of pure gold must be added to five ounces of something that is 1% gold in order that the mixture is 6% gold?
First off, it helps to know that mathematically, 25% of x is .25x
Before we start with any numbers though, the problem can be set up as:
w1 * f1 + w2 * f2 = w3 * f3 where
w is the total weight of each component and
f is the fraction of that component that's gold. (If that doesn't make sense, let me know and I can explain it a little more).
So, "something" #1 is pure gold (100% gold, or 1.00 gold), but we don't know the weight. "Something" #2 is 1% gold (.01 gold) and weighs 5 ounces. "Something" #3 is 6% gold (.06 gold) but we don't know the weight.
w1 * 100% + 5 * 1% = w3 * 6% or
1*w1 + .01*5 = .06*w3 or finally
w1 + .05 = .06*w3
The other piece of info we have is that
w3 (the final weight in ounces of the something) is equal to w1 + 5. Substituting that in to the last equation:
w1 + .05 = .06 * (w1 + 5) or
w1 + .05 = .06*w1 + .3
Subtract .06*w1 from both sides and you get
.94*w1 + .05 = .3
Subtract .05 from both sides:
.94*w1 = .25
Divide both sides by .94 and you get
w1 = .266 ounces (approximately)
3) One number is five more than another number. Their sum is 285. What are they?
If we call the first number
X and the second number
Y, we can write
X + Y = 285
From the problem statement, X is five more than Y, or
X = Y +5, so
X + (X + 5) = 285
or
2*X + 5 = 285
Subtract 5 from both sides
2*X = 280
Divide both sides by 2
X = 140
4) Find the equation for the line passing through (2,1) with slope 5/2.
There's kind of a shortcut in the way this one's worded, but shortcuts are no good unless you know how to get there the long way

The equation for a line can be written
y = mx + b
where
m is the slope and
b is the y-intercept (the value of y when x=0)
We already have the slope (
m = 5/2 = 2.5, so we just need to find b. Since we know that the line passes through the point (2,1), then these x and y values must satisfy the line's equation. In other words, just plug that point into the line's equation and solve for b
1 = 2.5 * 2 + b
or
1 = 5 + b
Subtract 5 from both sides, and
b = -4
So the equation for the line is:
y = 2.5x - 4
When it comes to factoring equations with squares, there a couple of different forms to check to see if your equation fits, because they will make your job easier. The relevant one here is called "difference of squares", and that's when you have an equation that looks like:
a^2 - b^2
If so, it factors to
(a+b)*(a-b). It might not be immediately obvious, but your equation fits this form.
Since 36 = 6^2, 36x^2 is the same as (6^2)(x^2) which is the same as (6x)^2. Therefore, your "a" term is 6x.
The "b" term is pretty obvious here... 1 = 1^2, so your "b" term is 1.
So here's how it all flows:
36x^2 - 1 = (6x)^2 - 1^2 = (6x+1)*(6x-1)
The factored form therefore is
(6x+1)*(6x-1)
To convince yourself, try multplying it all out and seeing if it simplifies back down to 36x^2-1
Whew! time for a :draught2: